Why You Should Include Cyber Requirements In The Development Cycle

You can save your organization up to 1000 times what they are already paying in cyber security costs by simply defining cyber security requirements before you start building your next product. For just a fraction of the cost involved in addressing a cyber security breach, you can define reasonable cyber security requirements and their implementation approach.

Supporting the Cost Savings

NASA conducted a research study in 2004 titled "Error Cost Escalation Through the Project Life Cycle". They based their study using the traditional systems engineering development cycle to estimate the cost of a requirements error.

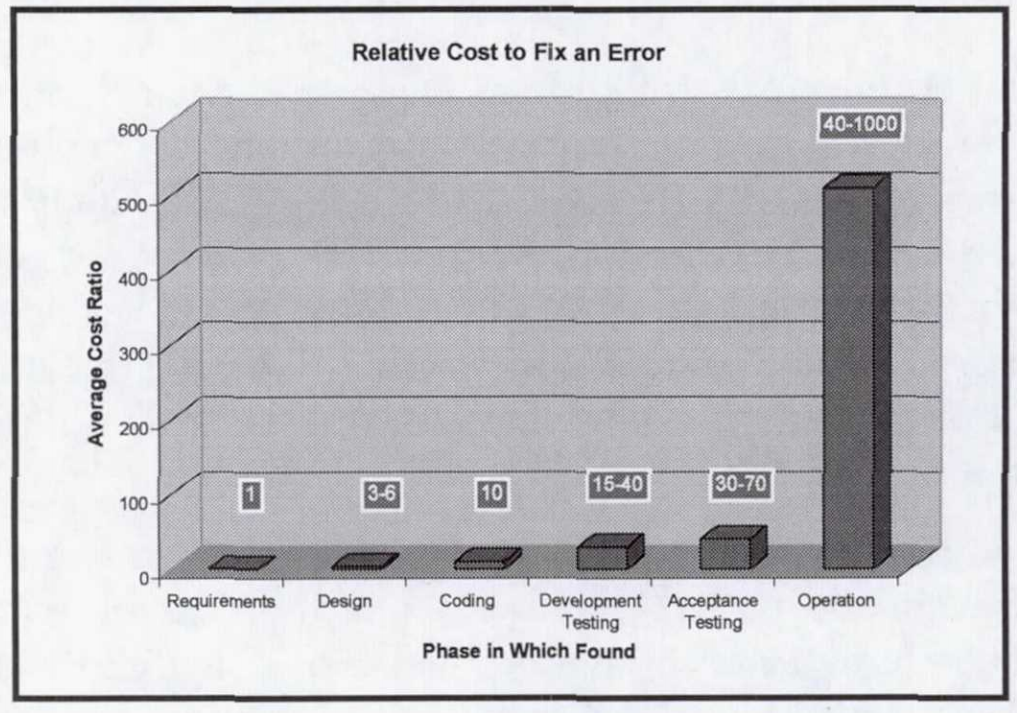
If you had one bad requirement defined during the requirements definition phase and you discovered the error, the cost to fix the error would be one time the cost of developing the requirement. If it was fixed in the coding phase, it would cost 10 times more. It would cost 40 to 1000 times more if it was fixed when the product was already in production.

During the recent 2018 Prime Day, there was a technical glitch discovered at launch which resulted in lost sales. It took over an hour before the error was repair and it cost Amazon millions in sales.

Not Having Any Requirements Is Defining Implicit Requirements

You might be wondering, "We don't have any cyber requirements. How can we say we are saving 40 to 1000 times if there are no requirements to correct?" That is an excellent point because many might state you cannot quantify what you do not have. I believe you can get a rough estimate by using the following logic:

Cyber Requirement #1: The system shall be open to cyber intrusions.

By not having any cyber requirements you have essentially defined the requirement above.

Cyber Error: The system becomes unusable due to a cyber breach.

We have defined a potential error for the requirement above.

Estimating the Cost of Not Having Cyber Requirements

What would be the cost to fix the error during the requirements phase? Let's assume you hire a cyber security expert consultant for one month to define basic requirements. Let's say that consultant charges a rate of $250,000 per year.

Your estimated cost for creating basic cyber security requirements during the requirements phase would be about $21K.

Now let's get the range of waiting until a breach occurs before defining and addressing the basic cyber requirements.

Your estimated cost for creating basic cyber security requirements during the operations phase would be about $833K to $20.8M.

According to a recent news article, the average cost for a cyber incident is $3.9M. Our estimate based on the NASA research is within a reasonable range. The cyber incident mentioned at the article cost $350M.

Requesting Your Budget

Your budget request should address the many financial concerns your leadership will have. Just to continue with our example above, you could give a very convincing argument like the one below.

Would it not behoove the company to spend 1% of the average cyber incident cost to hire a cyber security expert for 1.5 months to define cyber requirements? Yes, it will add a slightly higher cost and schedule delay. But would it not be better to spend a few percent more on cyber security and wait a few more months from a product launch than to pay several million dollars on a breach.

It seems to make sense when you put it into perspective.

Conclusion

Cyber requirements are important and it is even more important to address them early. You may be tempted to skip cyber security to get a product launched faster but it introduces a big financial and technical risk. The cost of cyber incidents will only continue growing. It is better to invest in cyber requirement as early in the development lifecycle.

Before You Go

A Note from the Author

Join my mailing list to get updates on my writings, my short stories, my upcoming books, and cybersecurity news. Visit https://miguelacallesmba.com/subscribe to join.

Stay secure,
Miguel

Main Image Credit : The awesome piece of artwork used to head this article is called 'RIP PC' and it was created by graphic designer AEDOS.